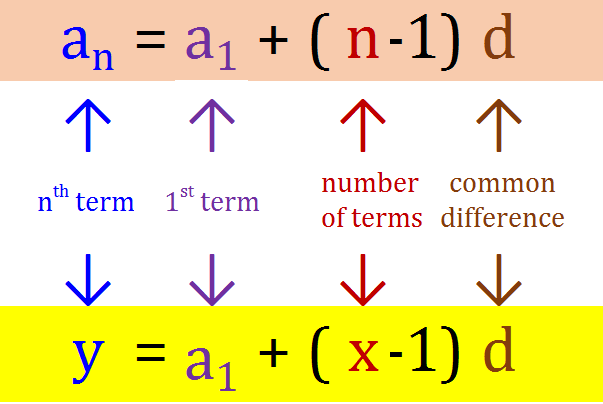Arithmetic Sequences
In mathematics, a sequence is an orderly set of numbers. Each element in a sequence is called term.
10, 15, 20, 25, …
10, 20, 40, 80, …
The times tables show some simplest sequences:
1,2,3,4,5, …
2,4,6,8,10, …
3,6,9,12,15, …
4, 8, 12, 16, 20 …
These three dots “…” are called ellipsis, and means that the sequence goes on forever (infinite sequence).
For example, 4, 8, 12, 16, 20 … make up the sequence that begins with the number 4, and increases by 4 each time. 4 is the first term, 8 is the second term, 12 is the third term, and so on.
An ARITHMETIC sequence has a common difference between terms. In this example, the common difference is 4.
After finding out the difference between the numbers, it becomes quite easy to identify additional terms in the sequence. Adding 4 to the previous number helps to arrive at the next number in the sequence, and thereby creates a pattern.
Terms in an arithmetic sequence:
a, a+d, a+2d, a+3d, … , a+(n-1)d
The first term is a, the common difference is d, and the number of terms is n.
Real world example:
The arithmetic sequence 4, 8, 12, 16, 24 … represents the total number of milk quarts that a store sold, after each additional gallon of milk is bought by the consumers.
RULES FOR SEQUENCES AND PATTERNS:
Find the Missing Numbers.
How may we find the missing numbers in a sequence?
First, we must identify a rule that relates to the sequence. From time to time, if we just look at the numbers we can see a pattern, thus the number sequence.
Pattern. A design (geometric) or sequence (numeric or algebraic) that is predictable because some aspect of it repeats ■□□□■□□□■□□□■□□□
Example 1: Toothpicks Pattern
The following pattern may be made with toothpicks, one for each straight line.
1 triangle = 3 toothpicks, 2 triangles = 5 toothpicks, 3 triangles = 7 toothpicks, ….
Each time we add one triangle, we need to add two more toothpicks. To add another triangle, we need to add two more toothpicks
Sequence 1: 3, 5, 7, 9, …
Difference: 2
Pattern: “add 2 to the previous number to get the next number”
Question: What are the next two terms in the sequence?
Answer: The next two terms are 9+2 = 11 and 11+2 = 13
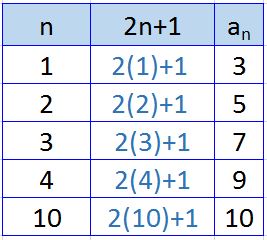
Question: Write an expression that can be used to find the nth term of the sequence 3, 5, 7, 9, …
Answer: The first term is a=3, the common difference is d=2, the nth term of the sequence is a+(n-1)d = 3+(n-1)2 = 3 + 2n -2 = 2n+1
Question: Find the 10th term of the sequence 3, 5, 7, 9, …
Answer: The first term is a=3, the common difference is d=2, the 10th term of the sequence is a+(n-1)d = 3+(10-1)2 = 3+(9)2 = 21
 SE01 Arithmetic Sequences Problems 1
SE01 Arithmetic Sequences Problems 1
SE02 Arithmetic_Sequences Problems 2
SE03 Arithmetic_Sequences_Rules
SE04 Geometric Sequences
SE05 Function Tables (Input-Output Tables )
SE06 Nth Term of an Arithmetic Sequence
SE07 Arithmetic Sequences
SE08 Arithmetic Sequences (Next Term)
SE09 Arithmetic Sequences Problems
SE10 Arithmetic Sequence (Nth Term)
SE11 Arithmetic Sequences (an)
SE12 Arithmetic Sequences (Recursive Formula)
EQ06 Function Tables (Find Slope )
EQ07 Find the slope of the line given two points
EQ08 Slope
EQ09 Find the slope and the y-intercept of each line.
Enrichment: Find the expression for the nth term, in the following pattern of squares made with toothpicks.
Graphing Arithmetic Sequences
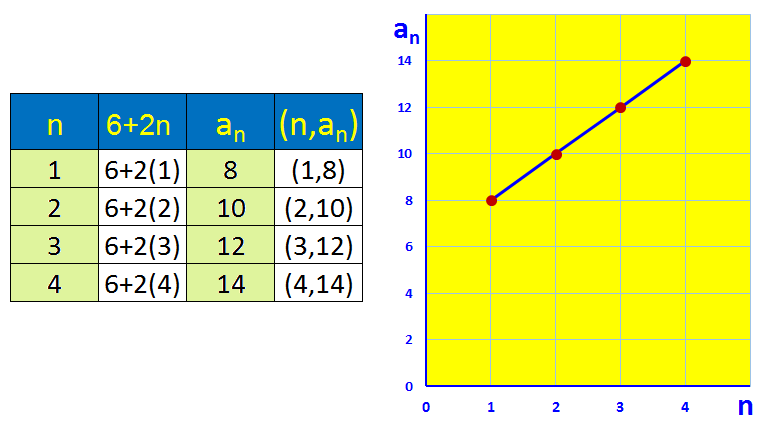
When we graph the points of an arithmetic sequence, they lie on a straight line.
All arithmetic sequences have linear graphs.
Example: A fair charges an entry fee of $6 and each ride is $2. The expression 6+2n tells us how much money we need to play n games.
The graph below shows the arithmetic sequence 6+2n
Arithmetic Sequence as a Linear Function
There is much resemblance between arithmetic sequences and linear functions.
An arithmetic sequence is a linear function whose domain is the set natural numbers (positive integers: 1, 2, 3, …), and the common difference is equivalent to the slope. However, an arithmetic sequence does not have a y-intercept (because n cannot be zero).
Linear functions are lines that continue forever in each direction, hence its domain is all real numbers (including integers, rational and irrational numbers).