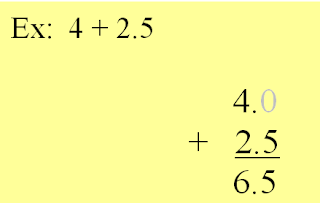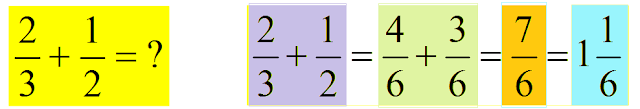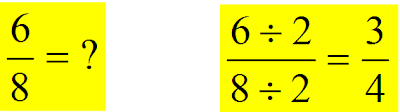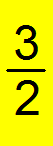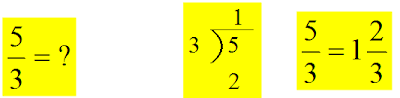Add, subtract, multiply and divide decimals and fractions; comparing and ordering rational numbers; graphing on coordinate grids including rational numbers
Decimal Numbers from Ms Garcia on Vimeo.
place value.
(2) Write place keepers if needed
(3) Add or subtract
(4) Keep your decimal point.
Introduction to Percentages from Ms Garcia on Vimeo.
Mixed Number. Whole numbers followed by fractions
Comparing and Ordering decimals.

Align decimal points and place values, write a place keeper if needed. (Pretend it’s money)
Percent formula
Example: 4% of 50 is____
Example: 10% of X is 15, find X
Percentage change between two numbers A & B can be calculated as:
(B-A)/A * 100
For example, if a game price increases in value from $10 to $12
the percentage increase is:
(12-10)/10 * 100 = 2/10 *100 = 0.2*100 = 20 percent
Alternatively, if a game price decreases in value from $10 to $9 the
percentage decrease is:
(10-9)/10 * 100 = 0.1*100 = 10 percent
Convert Fractions, Decimals, Percents
by the same number (10, 100, 1000, ..)
To convert a decimal to a percent, multiply the decimal by 100,
then add on the % symbol.
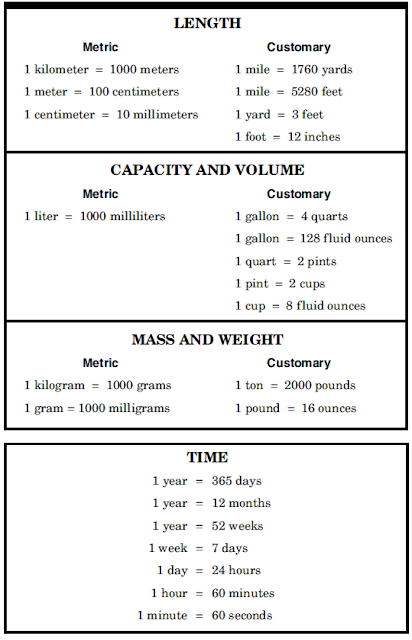
Conversion. Use the math chart. Do a proportion to solve.
Essential Questions:
How do I explain the meaning of a fraction and its numerator and denominator, and use my understanding to represent and compare fractions?
What strategies can be used to solve estimation problems with common and decimal fractions
Learning Targets:
Apply and extend previous understandings of multiplication and division to divide fractions by fractions
Solve word problems involving division of fractions by fractions.
Represent the context of a fraction word problem using a variety of models
Vocabulary:
decimal
place value
round
percentage
numerator
denominator
fraction
common fraction
proper fraction
improper fraction
mixed numeral
unit fraction
lowest common multiple
equivalent
“I can” Statements
I can add, subtract, multiply and divide rational numbers (including fractions and mixed numbers, with like denominators o with unlike denominators, with/without regrouping).
I can change freely between improper fractions and mixed numbers.
I can recognize if my answer is reasonable using estimation.
I can apply the commutative, associative, and distributive properties appropriately in multiplying and dividing rational numbers.
I can represent addition and subtraction on horizontal and vertical number lines.
I can subtract a rational number by adding its opposite (additive inverse).
I can use the absolute values of numbers on a number line to illustrate both addition and subtraction.
I can apply the properties of operations (commutative, associative, and distributive) to add and subtract rational numbers.
I can convert a fraction to a decimal using long division.
I can explain the difference between a rational and an irrational number.
I can add and subtract rational numbers in real-world situations.
I can use the four operations to solve problems involving rational numbers.
I can convert between whole numbers, fractions, and decimals.
I can estimate and compute in my head to determine whether an answer makes sense.