Rotation

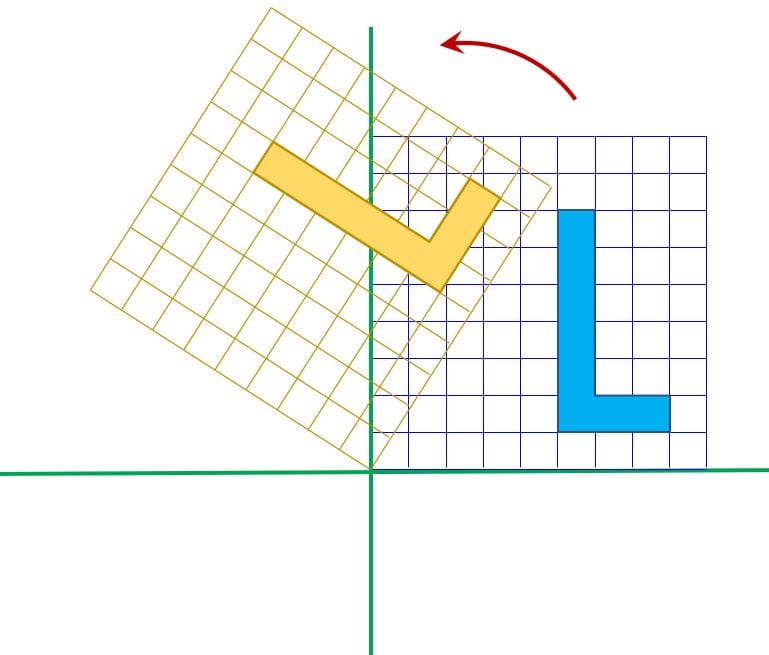
Rotation occurs when an object is turned around a fixed point.

This point is called the center of rotation.

We need three things to describe a rotation.

1) The direction of the rotation (clockwise [negative] or anti-clockwise [positive])

2) The angle: (90ᵒ (¼ turn), 180ᵒ (½ turn), 270ᵒ (¾ turn))

3) The center of rotation (this is the fixed point about which an object moves, always give as a coordinate).

When working in the coordinate plane, assume the center of rotation to be the origin.

————————————————————————————————————-

Clockwise means moving in the direction of the hands on a clock. “The clock hands rotate in a clockwise direction“.

Rotations in the coordinate plane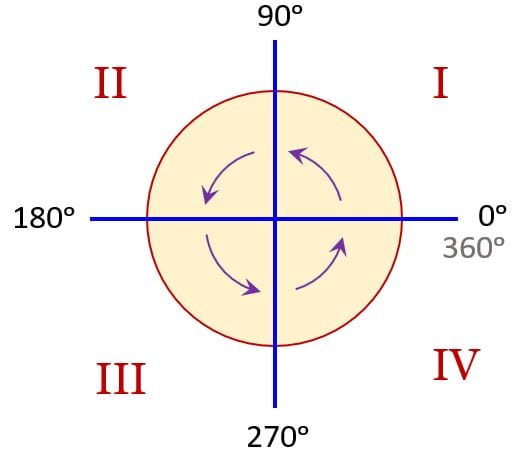

In a Coordinate Plane, angles are measured counterclockwise, as shown.

An angle measured counter-clockwise is positive, and an angle measured clockwise is negative.

Rotations (counterclockwise)

When a point rotates 90⁰, (a quarter turn) the X and Y values SWITCH places, and the Y becomes the opposite (sign changes).

***

The reason the X and Y values switch places is due to the X-axis and Y-axis switching places during the rotation. See the figure.

When a point rotates 180⁰ clockwise, you will need to apply the rule (x, y) → (-x, -y).

In other words, the coordinates are the same, but the signs are different.

When a point rotates 270⁰, (three-quarters turn) the X and Y values SWITCH places, and the X becomes the opposite (sign changes).