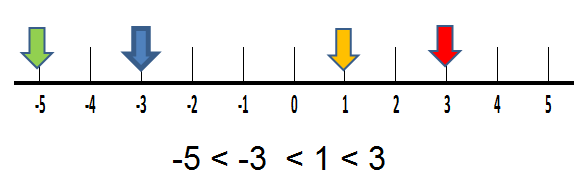Classifying numbers; identifying opposites; absolute values; locating & comparing integers; add, subtract, multiply, and divide integers; modeling integer operations; intro to coordinate grids.
In the review of this unit, we will be discussing sets of numbers, integers operations, and integers on the coordinate grid.
Includes positive numbers and negative numbers.
Also the neutral number zero
Real Numbers. The set of all numbers that can be represented by points on a number line.
Rational Number. Is a real number that can be expressed as the ratio of two integers {n/m}
(Rational numbers are whole numbers, fractions, and decimals )
Irrational Number. Is a real number that is not a rational number (it cannot be expressed as the ratio of two integers)
System of Real Numbers from Ms Garcia on Vimeo.
On a number line, positive numbers are to the right of zero. Negative numbers are to the left of zero. Zero is neither positive nor negative.
Opposites. Two integers that lie the same distance from the origin in opposite directions.
For example, “-3” (negative 3) is the opposite of “-3” (positive 3).
Absolute Value: A number’s distance from zero on a number line
We can use the number line to compare and order positive and negative numbers.
Going from left to right, numbers increase in value.
Going from right to left, numbers decrease in value.
The Number Line from Ms Garcia on Vimeo.
Compare Numbers on a Number Line from Ms Garcia on Vimeo.
Compare and order Integers
We can compare different integers by looking at their positions on the number line. For any two different places on the number line, the integer on the right is greater than the integer on the left.
Ex. Order 3, 5, -3, 1, -5
Operations with Signed Numbers
- If the signs of the numbers are the same, ADD. The answer has the same sign.
- If the signs of numbers are different, SUBTRACT. The answer has the sign of the larger number.
Factors. Numbers that are multiplied.
Ex: 2 * 3 = 6 the 2 and the 3 are factors of 6
(A diagram used to show the prime factors of a number.)
because they are all prime numbers.
Positive, negative and zero exponents with a base of ten
1/10000 = 0.0001 = 1 x 10⁻⁴
Scientific notation
Comparing and Ordering decimals.
The Coordinate Plane from Ms Garcia on Vimeo.

You can find more information on the following pages:
- Absolute Value
- Addition and Subtraction
- Compare
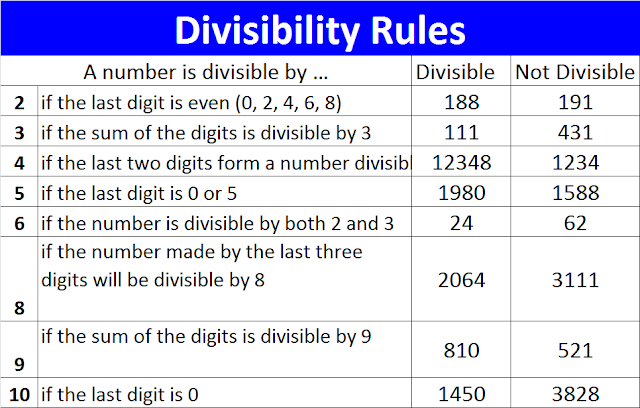
- Divisibility Test
- Multiples
- Multiply and Divide
- Powers of Ten
- Rounding
———————————————————————————-
Understandings:
- Know the Real Number System (know what relationships exist between the various subsets of rational numbers).
- Plotting numbers on number lines.
- Comparing and ordering numbers.
- Fluently, add, subtract, multiply, and divide rational numbers.
Vocabulary:
- Divisor, dividend, quotient, factor, product, sum, difference, numerator, denominator, subsets, sets, real numbers, rational numbers, irrational numbers, whole numbers, integers, terminating decimals, nonterminating decimals, repeating decimal, Venn diagram.
- Bar notation, common denominator, least common denominator, like fractions, rational numbers, repeating decimal, terminating decimal, unlike fractions.
Learning Targets:
- The Number System.
- Compute fluently with multi-digit numbers and find common factors and multiples.
- Fluently add, subtract, multiply and divide multidigit decimals
- Locate and plot rational numbers on a number line (horizontal and vertical) and a coordinate plane.
- Graph points in all four quadrants of a coordinate plane
- Find distances between points using my knowledge of coordinates and absolute value.
- Draw polygons in the coordinate plane.
- Identify the length of a side using coordinates.
- Solve real-world problems involving coordinate planes.
- Graph points in all four quadrants of a coordinate plane.
- Find distances between points using my knowledge of coordinates and absolute value.
- Find the greatest common factors of two whole numbers (up to 100)
- Find the least common multiple of two whole numbers (less than or equal to 12)