Natural Numbers: {1, 2, 3, 4, …} or Counting Numbers
Whole Numbers: {0, 1, 2, 3, 4, …}
Integers: {… -4, -3, -2, -1, 0, 1, 2, 3, 4, … }
Includes positive numbers and negative numbers.
Also the neutral number zero
Number Line
Absolute Value: A number’s distance from zero on a number line
Real Numbers. The set of all numbers that can be represented by points on a number line.
Rational Number. Is a real number that can be expressed as the ratio of two integers {n/m}
(Rational numbers are whole numbers, fractions, and decimals )
Irrational Number. Is a real number that is not a rational number (it cannot be expressed as the ratio of two integers)
Comparing numbers
Operations with Signed Numbers
Addition.
- If the signs of the numbers are the same, ADD. The answer has the same sign.
- If the signs of numbers are different, SUBTRACT. The answer has the sign of the larger number.
Subtraction. Change subtraction to addition of the opposite number.
Multiplication and Division. Multiply or Divide.
If the numbers have the same sign the answer is POSITIVE.
If the numbers have different signs the answer is NEGATIVE.
Factors. Numbers that are multiplied.
Ex: 2 * 3 = 6 the 2 and the 3 are factors of 6
Prime Factorization. Do the factor tree
(A diagram used to show the prime factors of a number.)
The prime factorization of 24 is 2 * 2 * 2 * 3,
because they are all prime numbers.
Exponent. A little number that tells you how many times you multiply a number by itself.
Ex. 8 = 23
Greatest Common Factor GCF. Do the factor tree for the given numbers and find what they have in common.
Ex. Find the GCF of (8,12)
8 = ②*②* 2
12 = ②*②* 3
The GCF of (8,12) is 4
Least Common Multiple LCM. Is the lowest number that can be divided both. Use the answers of the multiplication tables of the given numbers and find the smallest number they have in common. Ex. Find the LCM of (8, 12)
8, 16, 24, 32, 40, 48
12, 24, 36, 48, 60, 72
the LCM of (8, 12) is 24
Prime Numbers. Numbers that can only be divided by 1 and itself and have no remainders.
Prime Numbers = 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,
Composite Numbers. Numbers that can be divided by more than two factors and have no remainders.
Composite Numbers = 4, 6, 8, 10, 12, 14, 16, 18, 20, .
Neutral Numbers. These numbers are not prime nor composite: 0 and 1
Rounding Numbers.
(1) Underline the number that is in the place that you want to round
(2) Look at the number on the right of the underlined number.
* If it’s 5 or more, add one more to the underlined number.
* If it’s 4 or less, keep the underlined number the same.
(3) Numbers on the left stay the same and numbers on the right became zeros.
Ex. Round to the nearest hundreds
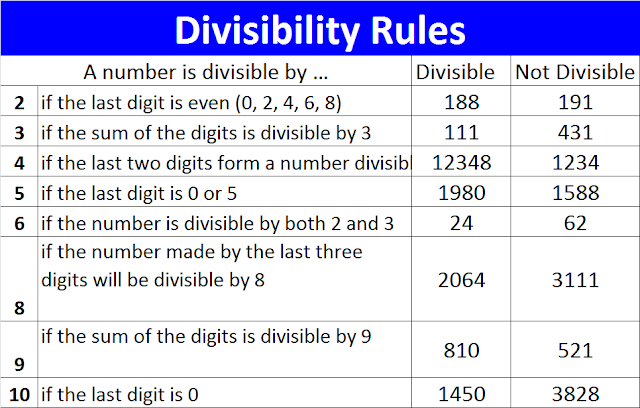
Divisibility Rules
Fraction. A part of a whole n/m
Decimal. Fraction with adenominator of 10, 100, 1000, …
Repeating Decimal. Is a decimal fraction in which the digits endlessly repeat a pattern, such as 1/3 = 0.3333333333333
Terminating Decimal. Is a fraction whose decimal representation contains a finite number of digits.
Place Value. It’s determined by its position with respect to the decimal point.

Positive, negative and zero exponents with a base of ten
10000 = 1 x 10⁴
1000 = 1 x 10³
100 = 1 x 10²
10 = 1 x 10ᴵ
1 = 10⁰
1/10 = 0.1 = 1 x 10⁻ᴵ
1/100 = 0.01 = 1 x 10⁻²
1/1000 = 0.001 = 1 x 10⁻³
1/10000 = 0.0001 = 1 x 10⁻⁴
Scientific notation
For example, instead of writing 65,000,000, we write 6.5 x 10⁷
Comparing and Ordering decimals.
Align decimal points and place values, write a place keeper if needed. (Pretend it’s money)
Add/Subtract decimals. (1) Align your decimal point and
place value.
(2) Write place keepers if needed
(3) Add or subtract
(4) Keep your decimal point.
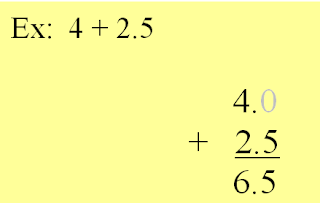
Adding/Subtracting Fractions.
(1) Find the common denominator by finding the LCM of the
denominators.
(2) Find your new fractions with the new denominator by using cross
multiplication.
(3) Add or subtract only the numerators. The denominators stay the
same.
(4) Simplify if necessary or change to a mixed number.
Simplify (reducing).
(1) Do the factor tree for both numbers.
(2) Find what they have in common and divide numerator (top) and
denominator (bottom) by that number, therefore renaming it to an
equivalent fraction in lower terms.
6 = ② * 3
8 = ② * 4
the GCF of (6,8) is ②
Multiplication of Fractions.
(1) Multiply the numerators (tops) and multiply the denominators
(bottoms),
(2) then reduce the answer to lowest terms.
Division of Fractions.
(1) Change division to multiplication by the reciprocal
(2) Multiply,
Mixed Number. Whole numbers followed by fractions
Improper Fractions. Are fractions that have a numerator (top larger than the denominator (bottom)
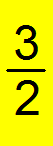
Conversions:
Mixed Number to Improper Fractions.
(1) Multiply the denominator with the whole number.
(2) Add the numerator to the product 1*3+2 = 5
(3) The sum is the new numerator
(4) The denominator stays the same.
Improper Fractions to Mixed Number.
(1) Divide. The numerator goes inside the radical and the
denominator goes outside.
(2) The quotient is the whole number.
(3) The remainder is the numerator.
(4) The denominator stays the same.
(5) Simplify if necessary. If there is no remainder, there is no
fraction.
Ratios. A comparison of two things.
It has 3 forms: 2 to 3 2/3 2:3
Rate. Ratio of two measurements with different units (miles/gallon, $/pound)
Unit Rate. Rate with a denominator of one. (50 miles / hour)
Cross Product. The product of the numerator of one fraction and the denominator of the other fraction.
Proportions. Statement of equality between two fractions or ratios.
A fraction (ratio) equal to another fraction (ratio).
To be a proportion the cross products must be equal
Ex. The ratio of dogs to cats is 3 to 2. If there are 10 cats, how many dogs are there?
õõõ / öö
Percents. Means “per 100”. Percents can be written as fractions by placing the number over 100 and simplifying.
Percents. Percents can be written as decimals (1) moving the
decimal point 2 places to the left, and (2) deleting the percent sign.
Percent formula
Example: 4% of 50 is____
or 50 x 4% = 50 X 0.04 = 2
Example: 10% of X is 15, find X
X*10%=15
X=15/10% = 15/0.10=150
Percent change
Percentage change between two numbers A & B can be calculated
as:
(B-A)/A * 100
For example, if a game price increases in value from $10 to $12
the percentage increase is:
(12-10)/10 * 100 = 2/10 *100 = 0.2*100 = 20 percent
Alternatively, if a game price decreases in value from $10 to $9 the
percentage decrease is:
(10-9)/10 * 100 = 0.1*100 = 10 percent
Convert Fractions, Decimals, Percents

Move the decimal point twice to the right
Move the decimal point twice to the left,
delete the percent sign
Write down the decimal divided by 1
Multiply its numerator and denominator
by the same number (10, 100, 1000, ..)
Simplify if necessary
To convert a decimal to a percent, multiply the decimal by 100,
then add on the % symbol.
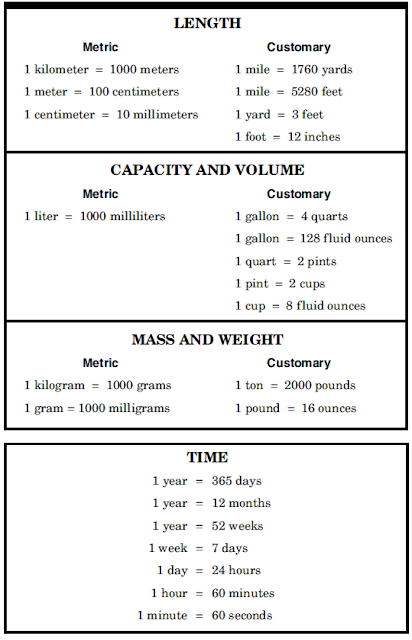
Conversion. Use the math chart. Do a proportion to solve.
Ex. How many centimeters are in 2.5 meters?
Now cross multiply 1 * X = 100 * 2.5 = 2500
There is 2500 centimeters in 2.5 meters
Perimeter. It is the distance around a figure. Add all sides.
Keywords: fencing, framing, edge, border.
Circumference. It is the distance around a circle. Use the chart. Keywords: fencing, framing, edge, border.
C = p d C = 2 p r
p Could be 3.1416, or 3.14, or 22/7, or 3 if it is an approximation. Approximately 3 diameters equal to the circumference of the circle.
r Radius is half of the diameter
d Diameter equals to two radius (radii)
Area. It is the surface space inside a figure (see the chart). Keywords: Painting, putting grass, putting tiles.
It uses a little two as the exponent. Ex: 4 m2
The measure of the interior region of a three-dimensional figure.
It uses a little 3 as the exponent. Ex: 250 cm 3.
Sequence. Is a set of numbers in which the numbers have a prescribed order.
10, 15, 20, 25, …
10, 20, 40, 80, …
Pattern. A design (geometric) or sequence (numeric or algebraic) that is predictable because some aspect of it repeats ■□□□■□□□■□□□■□□□
2, 4, 8, 16, 32, 64,…
Expressions/Equations. Equations have equal signs,
expressions don’t.
If you need to find an expression/equation from a table,
look at the pattern that goes from left to right.
A Monomial is an algebraic expression containing only one
term. For example: 3x2
A Polynomial is the sum of monomials (having different degrees)
A Binomial is he sum or difference of 2 monomials having different degrees. For example: 4x + 3
Always check what each variable (letter) represent.
Order of operations: mnemonic PEMDAS
Please Excuse My Dear Aunt Sally
Parentheses, Exponentiation, Multiplication, Division, Addition, Subtraction
Word Problems. · Read them as many times as you have. ·
Pretend you are the person in the word problem. · Draw a
picture if necessary. · Look for a pattern. · Read the question
again to make sure your answer makes sense and that you
answer it correctly.
Angles. The symbol for angles is Ð
Acute. More than 00 but less than 900 Ð
Right. Exactly 900 ∟
A small square inside angle means 900
Obtuse. More than 900 but less than 1800
Straight. Exactly 1800
Complementary angles Two angles whose measures have a
sum of 90° (e.g., 50° and 40° are complementary angles).
Supplementary Angles. Two angles whose measures sum to
180°.
Measuring angles with protractor. Find out how wide the
angle opened. Remember:
Use the top only (or bottom only) numbers for both sides.
You can NOT mix them.
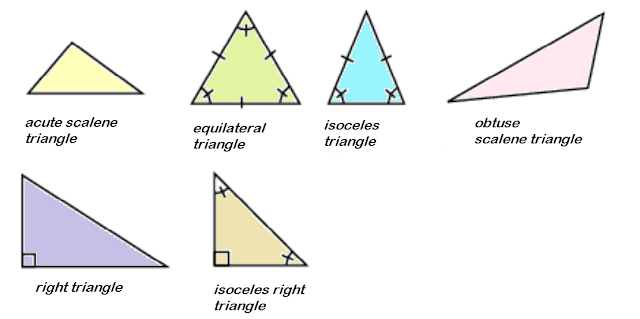
Triangles
Scalene. No equal sides nor angles
Isosceles. Two equal sides and 2 equal angles
Equilateral. 3 equal sides and 3 equal angles which are 600
each.
Right. 1 right angle, 2 acute angles
Acute. 3 acute angles
Obtuse. 1 obtuse angle, 2 acute angles
The interior angles of a triangle always add up to 180°
Polygon. A closed shape made up of at least 3 line segments. Ex. Triangle, Rectangle,…
Polygon. # Sides = # Angles = # Vertices
Regular Polygon. All the sides have the same length in that shape. Ex: Square, Pentagon,
Quadrilateral A polygon (plane figure) with 4 angles and 4
sides; the 4 angles sum 3600
Quadrilateral Family
Any four-sided shape is a Quadrilateral
A trapezoidis a polygon with four sides, two of which (the bases) are parallel to each other.
A parallelogram is a quadrilateral with two pairs of parallel sides.
Kite: two pairs of adjacent sides are of equal length.
Rhombus: all four sides are of equal length.
Rectangle: all four angles are right angles
Square (regular quadrilateral) The Interior Angles of a Quadrilateral add up to 360°
Parallel Lines. Two lines in a plane that do not intersect. ║
Perpendicular Lines.Lines meeting at right angles. ┼
Congruent. Two figures are said to be congruent if they are the same size and shape
A transformationis a change in position, shape, or size of a figure
Similar figures. Figures with same shape. They are not necessarily the same size.
Reflection. A reflection is a flip over a line. Every point of the original figure is the same distance from this line as is corresponding point of the reflected image. Every reflection has a mirror line.
A reflection of an “R” is a backwards “R”.
Slide/Glide To translate an object means to move it without rotating or reflecting it. Every translation has a direction and a distance.
Rotation. A rotation is a turn of a figure around a point. The point can be on or in the figure, or outside the figure.
Geometric Similarity
Figures that have the same shape but not necessarily the same
size are similar. Necessary conditions:
1. Corresponding angles of the figures must be congruent (equal)
2. Corresponding sides of the figures must be proportional.
Graphs. Read the title and the labels. Look for the key, if there
is one. Look at the scale (is it going by 2’s, by 10’s, by 100’s)
Coordinate Plane. It is made up the X-axis and Y-axis. To find a point on the plane, find the number on the corresponding axis and check where they meet.
X Y
( 2 , 3 )
Probability. It is the chances that something is going to occur. It could be written as a fraction or %.
Ex: A single die is tossed.
What is the probabilityof a 2 turning up
Combinations. Do a tree diagram or multiply what you are going to combine. Ex. How many combinations can you make with a blue and a red shirt and a black and a white pant?
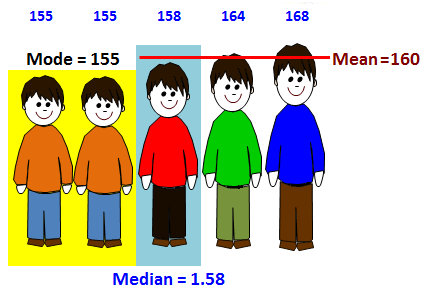
Mean. The average. (1) Add all the numbers (2) Divide the sum by the amount of numbers given.
Median. Order the numbers, and then find the middle. If 2 numbers are in the middle add and divide by 2.
Mode.The number that occurs most frequently
(Repeat the most)
Range. Subtract the largest minus the smallest. (Max – Min)
An inequality says that two values are not equal.
a < b says that a is less than b
a > b says that a is greater than b
a ≤ b says that a is less than or equal to b
a ≥ b says that a is greater than or equal to b
Proportional relationships
Two variables are proportional if a change in one is always
accompanied by a change in the other.
Directly Proportional
The equations of such relationships are always in the form
Y = m•X , and when graphed produce a line that passes through
the origin. In this equation, “m” is the slope of the line (or
coefficient of proportionality, unit rate, rate of change).
Inversely proportional
Inversely proportional means that one variable goes up while the
other goes down.
3 workers paint a house in 12 hours. How long would it have
taken for 9 equally productive workers?
If Y is inversely proportional to X, the equation is of the form
Y·X = k (where k is a constant). Y=k/X
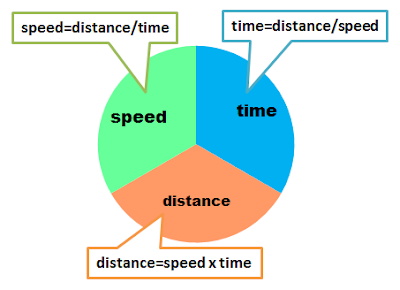
Speed and time are inversely proportional because as the speed
increases, the time it takes to reach the destination decreases.
David travels 120 miles at 40 mph.
How long does it take him?















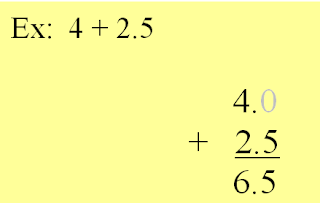
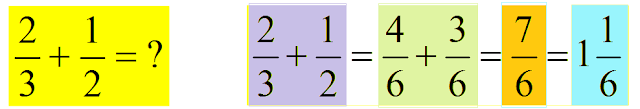
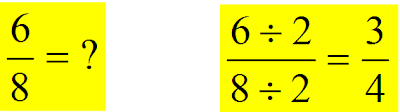



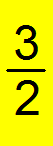

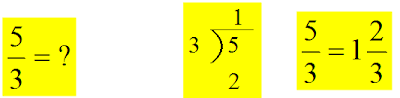

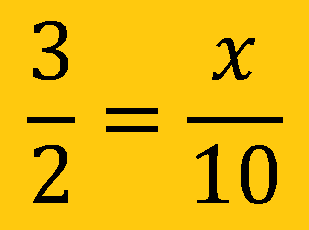

















.gif)