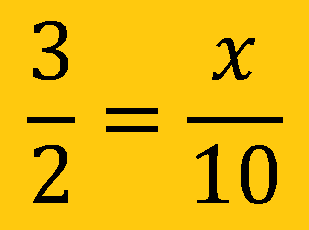Identifying additive/multiplicative relationships; ratios, percents, proportions, scale factor, part-whole-percent problems
Ratios. A comparison of two things.
It has 3 forms: 2 to 3 2/3 2:3
Rate. Ratio of two measurements with different units (miles/gallon, $/pound)
Unit Rate. Rate with a denominator of one. (50 miles / hour)
Cross Product. The product of the numerator of one fraction and the denominator of the other fraction.
Proportions. Statement of equality between two fractions or ratios.
A fraction (ratio) equal to another fraction (ratio).
To be a proportion the cross products must be equal
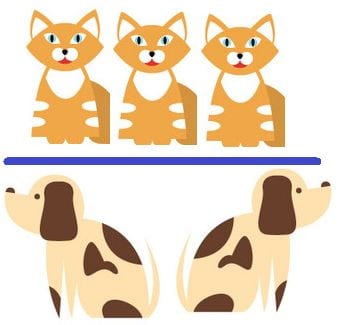
Ex. The ratio of dogs to cats is 3 to 2. If there are 10 cats, how many dogs are there?
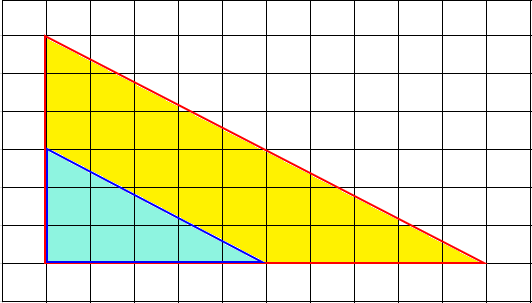
Similar figures are the same shape, but not necessarily the same size.
Scale factor is the ratio of corresponding side lengths.
If the scale factor is two, then the perimeter of the new object will be two times the perimeter of the original figure.
If the scale factor is two, the area of the new object will be four times (two squared), the area of the original figure.
Geometric Similarity
Figures that have the same shape but not necessarily the same size are similar. Necessary conditions:
- Corresponding angles of the figures must be congruent (equal)
- Corresponding sides of the figures must be proportional.

There are three basic types of percent problems:
Find the percent
4 is what percent of 8?
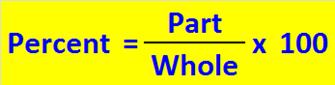
Find the part
What number is 50% of 8?

Find the whole
4 is 50% of what number?

Essential Questions:
How can problems involving ratios and rates be solved without using a proportion?
What is the relationship between a ratio and a proportion?
How does a proportion compare two equivalent ratios?
How is the ratio or rate used to compare two quantities or values?
Learning Targets:
-Explain the concept of ratio.
-Describe the relationship between two quantities using ratio language.
-Explain the relationship between rate, ratio, and percent.
-Solve word problems using ratio and rate reasoning.
-Understand ratio concepts and use ratio reasoning to solve problems
Understandings:
Ratios and rates can be used to express the relationship between two different quantities.
Know how to solve proportional reasoning with ratios and rates, and how to verify their answer.
Know how to write ratios in simplest form.
Know how to compute and use a unit rate to solve real-life problems.
Equivalent equations and proportions are equal
Equivalent ratios are equal
There is a proportional relationship between parts of a ratio.
“I can” Statements
I can write a ratio as a part-to-part or part-to-whole in different ways (a:b, a to b, a/b).
I can explain what a part-to-part or part-to-whole relationship means in a given situation.
I can use models and pictures to relate concepts of ratio, proportion, and percent.
I can represent and analyze patterns, rules, and functions using tables, graphs, words, and manipulatives.
I can determine whether two quantities represent a proportional relationship.
I can recognize, represent, and explain proportions using tables, graphs, equations, diagrams, and verbal descriptions).
I can determine the appropriate unit rates to use in a given situation, including those with fractions.
I can compute unit rates.
I can transfer my understanding of unit rates to multiple real-world problems.
I can explain what a point (x, y) on the graph of a proportional relationship means in terms of the situation, with special attention to the points (0, 0) and (1, r) where r is the unit rate.