Area of parallelograms, trapezoids, and triangles; volume of right rectangular prisms

Polygon.  A closed shape made up of at least 3 line segments. Ex. Triangle, Rectangle,…

Polygon.      # Sides =  # Angles = # Vertices

Regular Polygon.  All the sides have the same length in that shape. Ex: Square, Pentagon,

Quadrilateral   A polygon (plane figure) with 4 angles and 4    sides;  the 4 angles sum 360⁰

Any four-sided shape is a Quadrilateral

 

Quadrilateral Family

 

A trapezoid is a polygon with four sides, two of which (the bases) are parallel to each other.

 

A parallelogram is a quadrilateral with two pairs of parallel sides.  

 

Kite: two pairs of adjacent sides are of equal length.

 

Rhombus: all four sides are of equal length.

Rectangle: all four angles are right angles

 Square (regular quadrilateral) The Interior Angles of a Quadrilateral add up to 360°

 

 

 

 

 

 

 

 

 

Solids

Solid:. A three-dimensional object. The 3 dimensions are called width, depth, and height.

Cube.  A prism with six congruent faces.

Opposite faces are parallel.

6 Faces (each face is a square)

12 Edges

8 Vertices (corner points)

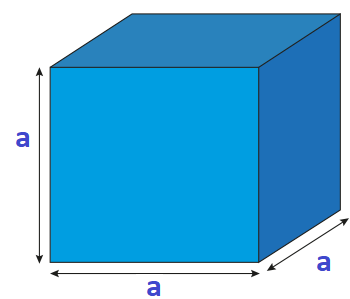
The surface area of a cube is the area of the six squares that cover it.  (Surface Area = 6 a²)

Volume of a cube = a³     (Volume=side times side times side).

 

 

Volume of a rectangular prism

The formula for finding the volume of a rectangular prism is the following:

Volume=length×width×height

 

The formula to find the surface area of a rectangular prism is

A = 2wl + 2lh + 2hw,

 

 

 

Essential Questions:

What is volume and how does it relate to the attribute of an individual figure?

 

Learning Targets:

• Find the area of polygons by composing or decomposing them into basic shapes.
• Apply my understanding of shapes to solve real-world problems.
• Solve real-world and mathematical problems involving area, surface area, and volume.
• Solve real-world and mathematical problems involving area, surface area and volume.
• Explain the volume formula of a rectangular prism using unit cubes.
• Find the volume of a rectangular prism using formulas.
• Solve real-world problems involving volume.
• Represent three-dimensional shapes using nets.
• Find the surface area of three-dimensional shapes (using nets).
• Solve for surface area in real-world problems involving three- dimensional shapes.

Understandings:

• The perimeter is a linear measurement, and the area is not.
• Develop an understanding of circumference and area of a circle.
• Formulas can be used to calculate circumference and area of two-dimensional shapes.
• Pi represents the constant relationship between the circumference and the diameter of all circles.

Vocabulary:

• Circle, Pi, diameter, radius, circumference, area, rectangle, square, parallelogram, trapezoid, triangle, semicircle, quarter circles, composite figure, triangle, angle